수학이 정말 많이 나온다...
근데... 교수님 피셜 수식을 하나하나 알아야 아는것보단 큰그림 빅 픽 쳐 를 그리는 게 더 중요하다고 하시고
그냥 수식을 하나하나 한번정도 봐두는 것은 추천한다고 하신다..
나는.. 수학을 따라가려고 노력했는데.. 보시는 여러분도 한번쯤.. 해보시길
2.9 요약
전방향 신경망 학습을 비롯한 기본적인 것들
경사 하강법, 역전파 알고리즘, 과적합 방지 방법
2.1 패스트푸드 문제
아직까지의 의문점, 파라미터 벡터(θ, 신경망 내 연결에 대한 가중치)가 무엇이 되어야 하는지 어떻게 알아내는가?
=> "학습"을 통해 알아낼 수 있다.
많은 예제를 통해 학습하면서, 예제들에 대한 오차를 최소화하며 가중치를 수정한다.
충분한 예제를 학습하면 해당 과제를 효율적으로 해결하는 파라미터 벡터를 가지게 되고
과제를 매우 효율적으로 해결할 수 있게 된다.
무슨 말인지 예제를 통해 더 자세히 알아보도록 하자
예제)
<문제 설명>
1.7 선형 뉴런과 그 한계에 나왔던 예제이다.
다음의 선형 뉴런은 햄버거, 감자튀김, 탄산음료 3가지를 주문받고 조합된 가격(Y)을 출력한다
(f(z) = z의 선형 함수를 사용한다)

패스트푸드 식당에서 햄버거/감자튀김/탄산음료로 구성된 세트를 주문하면,
각각 단품 개수에 따라 돈을 낸다. 각각 단품의 가격은 알 수 없고 오직 세트의 가격만 알 수 있다.
쉽게 그림으로 설명하면 이러하다
n개의 세트로 구성된 메뉴가 있는데, 단품은 팔지 않아 단품의 가격을 알 수 없다
(햄버거/감튀/음료의 종류는 1가지 개수만 다르게 구성된 세트이다.. 아주 게으른 패스트푸드점인 모양)

이를 해결하기 위한 선형 뉴런 모델은

이러하다
여러 개의 세트메뉴의 구성과 가격을 학습시켜서 오차가 최소한이 되는 단품의 가격(가중치 w / 최적화 파라미터 벡터)을 알아내려고 하는 것이다
여기서 f(z)=z이므로, 그 이유는 위 그림과 아래 식을 보면 알 것이다 ( 1개의 가격과 개수의 곱의 합이 곧 총액이므로)


이 되는 것이다.
이제 문제를 충분히 이해했으니 해결 방법을 살펴보도록 하자.
<1번째 방법 : 아주 이상적인 상황>
아주 간단한 방법은
각각 햄버거 1개, 감자튀김 1개, 탄산음료 1개로 구성된 세트메뉴를 따로따로 주문하는 것이다.(만약 존재한다면 말이다..)

이렇게 되면 3번의 주문 예시로 한 번에 w1, w2, w3 즉, 각각 1개의 가격을 알아낼 수 있다
하지만 이렇게 운이 좋은 경우는 흔하지 않으므로, 실제 상황에서는 거의 사용할 수 없다.
이 전략은 효과가 없으며 현실적인 해결책이 아니게 된다.
< 2번째 방법(전략) : 일반적으로 작동하는 방법 >
우리의 학습 신경망은 다음과 같고,

제공되는 training set(실제 사례, 실제 올바른 값)은 다음과 같다

그럼 우리의 학습 신경망은
사례를 하나하나 학습하면서, w1, w2, w3을 계속하여 더 좋은 값으로 갱신시킬 것이다.
이때, 더 좋은 값이란 실제 가격(t^(i))과 신경망이 계산한 가격(y^(i)) 의 오차가 더 적은 경우 일 것이다.
그리고 오차가 0이 되는 것(예상 값과 실제 값이 같아지는 경우)이 최적 파라미터 벡터 W = [w1 w2 w3] 일 것이다.
즉, 신경망은 오차를 최소화하는 가중치 w를 선택하기 위해 학습할 텐데 이는
이때 만나게 된(학습한) 모든 학습 데이터의 오차의 제곱을 최소화하는 방법으로 구할 수 있다.
모든 학습 데이터의 오차의 제곱을 E라고 하면,

다음과 같은 식으로 오차 함수 E를 나타낼 수 있고, E를 최소화 , 0에 가까울수록 더 좋은 모델이 되는 것이다.
사실 위의 예제는 학습이 아닌, 연립방정식으로 문제를 해결할 수 있다.
하지만 그러지 않는 이유는 일반화하기 어렵기 때문이다.
우리는 이미 1단원에서 세상에 많은 문제는 선형 뉴런으로 해결할 수 없다는 것을 알았다.
1.8에서 나온 시그모이드, tanh, ReLU 같은 비선형 뉴런을 사용하면 연립방정식을 사용할 수 없으므로,
학습 과정을 위한 더 좋은 전략(방법)이 필요함이 자명하다.
이제 앞으로 다양한 전략에 대해 알아보자
2.2 경사 하강법(Gradient Descent)
*Gradient (기울기 ) : 벡터의 각 요소로 편미분 한 것
경사 하강법을 제대로 들어가기 전에...
우리의 목표는 결국 오차 함수 E를 최소화하는 것이다.
특정 함수의 "최소"를 구하는 방법은 "미분 적분학"에서 배웠을 것이다.
기억이 안 날 수 있으니 쉽게 최대/최소부터 살펴보도록 하자
<일변수 함수>
일변수 함수에서의 극대, 극소
[ 어떤 열린 구간 I에 속하는 모든 x에 대하여, f(a)>=f(x)가 성립하면, f(a)는 f의 극대 값
f(a)<=f(x)가 성립하면, f(a)는 f의 극소값이라고 한다. ]
라고 정의되어 있지만, 미적분을 배울 당시 우리는 구간 I 내에서 연속이고
(a, f(a))를 지점으로 하여,
증가하던 함수가 감소하게 되면 그 점은 "극대"
감소하던 함수가 증가하게 되면, 그 점은 "극소"
라고 배웠다. 아래 그림을 참고하자
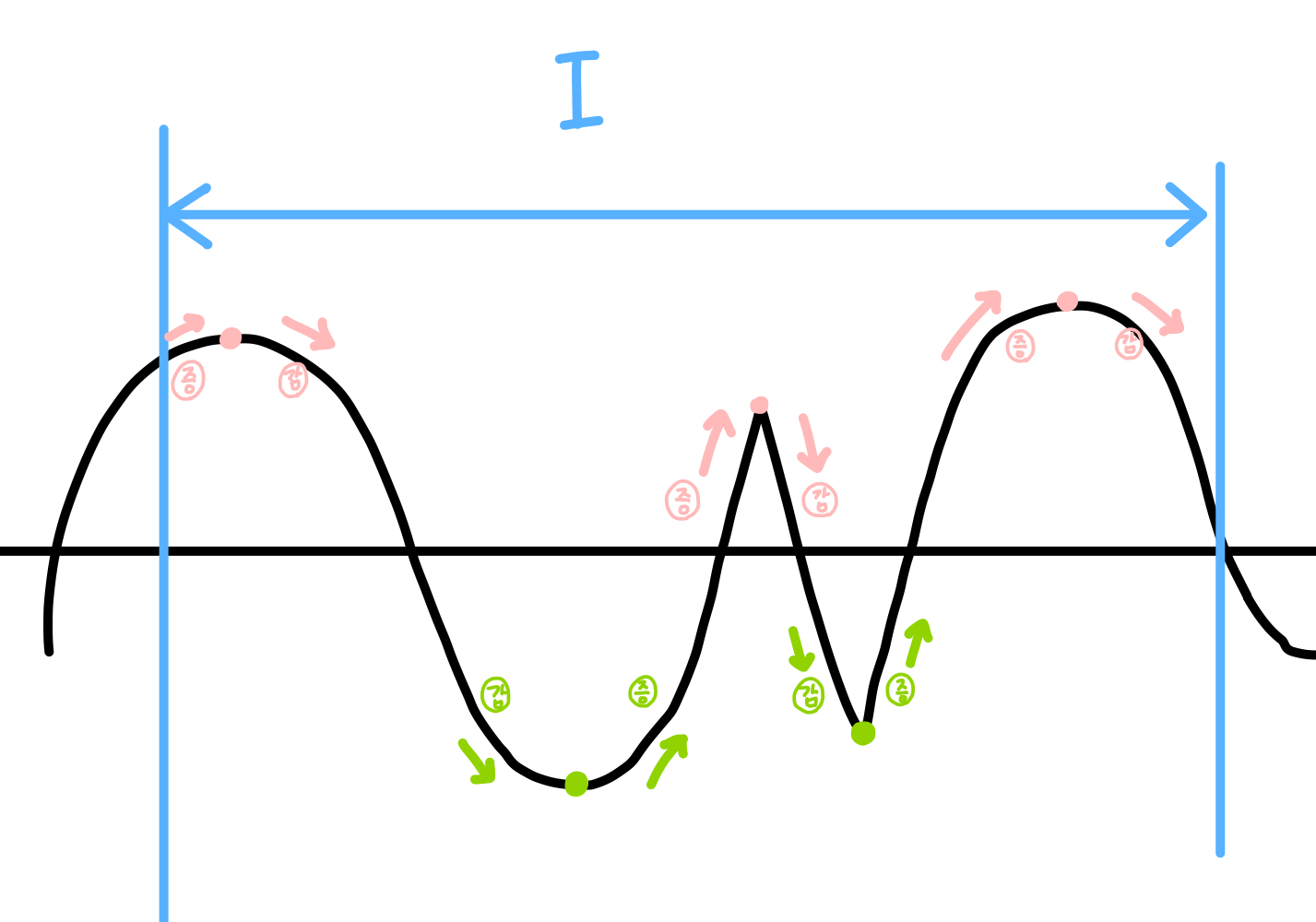
초록색 점은 극소, 붉은 점은 극대 (둘을 합쳐 극점이라고 한다)
라고 할 수 있다.
더욱 일반적으로 우리는 함수를 미분했을 때, f'(a) = 0이 되는 지점을 극점이라고 볼 수 있다
(물론 뾰족한 점은 미분할 수 없지만 그 점은 넘어가도록 한다)
왜 0인가는 생각해보면 쉽다, 값이 커지다가 작아지거나 작아지다가 커지려면 일단 증가량이 0이 되어야 하기 때문이다
마치 달리던 차의 방향을 반대로 바꿀 때 무조건 차의 속력이 0이 되는 지점이 오는 이치와 같다
우리는 함수의 최대/최소를
< 극점과 양 끝 값 중에서 값이 가장 크면 최댓값 , 값이 가장 작으면 최솟값 >으로 찾아냈다.
오차 함수가 1차 함수라면 참 좋겠지만.. 불행하게도 그럴 일은 거의 없다
오차 함수는 거의 다변수 함수 일 것이다
아래의 예제에는 다변수 함수로 등장한다
이변수 함수의 극값을 구하는 법을 잠깐 설명하고 가면
<정리> : 역은 성립하지 않는다
함수 f(x, y)가 점(a, b) 근방에서 fx, fy를 가질 때,
f가 점 (a, b)에서 극값을 가지면, fx(a, b)=fy(a, b)=0이다
이변수 함수에서 fx(a, b)=fy(a, b)=0을 가지는 점은
임계점, 안장점 두 개가 있는데
임계점은
1) fx(a, b) = fy(a, b) = 0 OR 2) (a, b)에서 fx나 fy가 존재하지 않는 경우이고,
안장점에 대해서는 자세히 말하지 않겠지만 안장점은 이변수 함수의 최대/최소를 구할 때 고려되지 않는다.
안장점은 극값이 아니기 때문인데, 이것이 바로 위의 역이 성립하지 않는 반례이다.
즉, 이변수 함수에서 최대, 최소를 구할 때는
임계점/양끝 값 중 가장 큰 값, 가장 작은 값으로 구한다
이렇게 2차함수 처럼 바로 구할수 있었으면 참 좋겠고...또한,
전체 함수를 알 수 있으면 참 좋겠지만 안타깝게도 우리는 전체 함수 E를 알지 못한다 //전체 데이터 셋을 알지 못하니까?
이 상황에서 어떻게 최솟값을 찾을 수 있을까?
그 방법이 경사 하강법이다.
이제 본격적으로 경사 하강법에 대해 알아보도록 하자
경사 하강법을 대충 비유하자면 이러하다.

어떤 사람이 그랜드 캐니언의 어딘가에 매달려있다.
그는 그랜드 캐니언의 지반이 가장 낮은 곳(낮은곳은 그래디언트의 반대방향이므로 -가 붙는다)으로 가고 싶은데
그랜드캐니언의 전체 모습이 어떤지도, 가장 낮은 곳이 어딘지도, 자신이 어디쯤 위치해있는지도 알지 못한다
그럼에도 지반이 가장 낮은 곳으로 가고 싶다면, 일단은 평평한 면을 만날 때까지 한발 한발 아래쪽의 경사를 따라 이동하는 수밖에 없다.
(여기서 의문은 평평한 면이라는 것은... 아마 지반이 가장 낮은 곳이 아니어도 존재할 것이다 그랜드 캐니언의 그림만 봐도 그러하다
근데 가장 낮은 곳으로 어떻게 가는가..? 는 아마 뒤에 나오지 않을까 싶다 일단은 그 문제는 접어두기로 하자 -> 2.6에 나오는 듯
4단원에 더 자세히 나오는듯 하네요 그떄까지 이 문제를 접어둡시다)
https://www.youtube.com/watch?v=IHZwWFHWa-w 이 영상을 보면 더 좋ㅇ르듯

그랜드 캐니언의 지반은 함수 E의 개형이고,
그랜드 캐니언에서 지반이 가장 낮은 곳은 E의 값이 최소가 되는 지점이다.
학습망의 현재 위치에서, 함수의 최솟값(평평한 면, 기울기 = 0)으로 한 스텝 한 스텝 이동하는 것이다.
그랜드 캐니언을 떠올리며 다음 예를 살펴보자.
선형 뉴런이 2개의 입력(w1, w2)만을 가진다고 가정한다.
즉, 오차 함수 E는 w1, w2 두 개의 변수를 가지는 이변수 함수이다.
함수 E(w1, w2)라고 볼 수 있고, 이는 E = w1과 w2에 관한 식이라고 보면 된다.
함수를 그래프로 표현하면 다음과 같다.

w1, w2의 값을 변경할 때마다 E의 값도 달라지는데
우리는 E를 최소화하려고 한다. 3차원 상의 그래프에서 E가 제일 작은 부분은 별 모양이 표시된 부분이라고 볼 수 있다.
이 곡면을 타원의 등고선들의 집합으로 시각화하여 보면 편하다.
등고선은 같은 같은 E값을 가지는 w1과 w2의 조합에 대응하는 것으로
E함수를 E=1 , E=2, E=3등 특정 E의 값을 가지는 평면으로 자르면 나오는 도형을 한 평면에 그려놓은 것이다

이 함수는 등고선을 그리면 아래와 같은 타원 등고선의 집합으로 표현된다

이렇게 표현되면 E가 최소인 부분(그래프 상에서 별 모양이었던 부분)은 타원의 중앙임을 알 수가 있다.
(처음 시작 위치는 수평면 위 어딘가로 무작위로 초기화(w1, w2가 무작위로 초기화된 상태) 되었다고 하자)
등고선이 서로 가까울수록 경사는 가파르다(가장 가파른 하강 방향은 등고선에 대해 수직)
경사(기울기)가 가파른 방향으로 한걸음 나아가다 보면 타원의 중앙에 도달할 수 있을 것이다.
이런 방법이 바로 경사 하강법(Gradient Descent)이다.
다음은 Xn-1에서 Xn으로 한 스텝을 나아갈 때의 식을 보여준다. //출처는 아래에

Xn-1에서 (그래디언트*학습률)을 뺀 값이 다음 스텝이다
**-가 붙는 이유: 미분하면 양수 값인데 이동해야 하는 것은 감소하는 방향이므로 마이너스가 붙음
위의 그림을 본 후 다음 단원으로 넘어가서 이게 뭔지 자세히 보도록 하자
2.3 델타 규칙(Delta Rule)과 학습률(Learning Rates)
위의 n-degree의 식을 다시 한번 살펴보자

학습률 * 그래디언트는 어디서 나온 것일까?
실제로 등고선에서 수직으로 이동하는 각 단계에서 새로운 방향을 재계산하기 위해
"얼마나 멀리 나갈지"를 결정해야 한다.
1. 그래디언트(어느 방향으로 내려갈 것인가?)
이는 곡면의 가파른 정도(기울기-그래디언트)에 의존하는데 ,
그 이유는 "최솟값에 가까울수록 앞으로 나가는 거리가 짧아진다"
즉, 아래 그림에서도 볼 수 있듯이 최솟값으로 갈수록, 곡면이 점점 평평해진다.
그렇기 때문에 곡면이 많이 평평해지면 최솟값에 근접해 있다는 사실을 알 수 있다.
이 때문에, 최솟값에 얼마나 가까운지에 대한 지표로 가파른 정도(그래디언트)를 사용한다.
이왕이면 가파른 쪽으로 내려가야 최솟값에 빠르게 도달할 수 있으니까!

+) 그래디언트
이변수 함수 f(x,... , xn)에 대해 f의 그래디언트는 다음과 같은 "벡터 함수"이다.
각각의 성분 벡터로 편미분 한 것이다.

2. 학습률(얼마나 많이 내려갈 것인가?)
신경망에서 정의한 가중치 파라미터 외에도 학습과정을 수행하기 위해서는
학습 알고리즘 또한 추가로 한쌍의 파라미터가 필요한데, 이를 하이퍼 파라미터(hyperparameters)라고 하고 그중 하나가 "학습률(Learning Rate)"이다.
하지만 오차 곡면이 매우 완만해지면 학습하는데 시간이 매우 오래 걸릴 가능성이 크다

그래서 경사에 학습률을 곱한다.
하지만 학습률을 너무 크게 잡으면 최솟값 근처에서 발산할 가능성이 높다.

등고선으로 보면,

학습률을 적절하게 선택해 주어야 하는데 이는 3장에서 자세히 (학습률 선택을 자동화하는 학습률 적응을 이용한 최적화 기법에 대해...)
델타 규칙
우리가 지금까지 E함수의 최소를 구하기 위해 배워온 것은
E(w1,... wn)을 최소 E값을 가질 때로 가중치(변수) w1,... wn을 모델에 더 좋은 값으로 갱신시키기 위해서라는 것을 다시 한번 상기하자.
각 가중치(w)를 어떻게 갱신할지 계산하기 위해 경사를 평가한다.
경사(Gradient = ΔWk(Wk가중치의 변화량))는 각 가중치에 대한 오차 함수의 편도 함수로 나타낼 수 있다.

가중치를 변경하는 이 방식을 모든 반복에 적용하면 경사 하강법을 이용할 수 있다.
+) 참고
k는 i= 1~n과 관계없고 m가 관계있다
패스트푸드 예제를 예로 들어보면(아래 그림 참고), w에 해당하는 k는 세트 메뉴의 구성 종류와 연관되었고, (햄버거/감자튀김/탄산음료)
i는 몇 번째 세트 메뉴인지와 연관 있는 수였음.
n가지의 세트 메뉴 중 i번째,
m가지의 세트메뉴 구성요소(햄버거, 음료, 감자튀김, 아이스크림... 등등 ) 중 k번째 단품의 가격 Wk

<(경사) 그래디언트>
경사 하강법 N-degree의 식을 다시 한번 보면

Xn-1이 Xn으로 변화될 때의 식이므로, 변화량은 Xn - Xn-1과 같다.

2.4 시그모이드 뉴런(Sigmoidal Neurons)의 경사 하강법
이번에는 빈선형을 활용한 신경망과 뉴런 학습을 다룬다. 모델로는 시그모이드 뉴런을 사용하기로 한다.
2.3까지는 2.1 패스트푸드 예제에서의 f(z) = z의 선형 함수를 사용했기 때문에,
y = f(z) = z 가 되었지만, 이제는 시그모이드 함수를 사용하기 때문에 , y는 다음과 같게 된다.

y의 값이 달라지는 것을 제외하면, 델타 규칙과 같다.
델타 규칙에 적용하면 다음과 같은데,

초록색 부분이 어떻게 나왔는지 설명하면,

이 예제에서는 계산을 쉽게 하기 위하여 bias항목을 사용하지 않았다
(z = WkXk + b의 시그마인데 b를 사용하지 않음)
dy/dz에 대해 자세히 알고 싶다면,

응용해서 tanh뉴런의 경사 하강법을 구해보자
tanh뉴런의 경사 하강법
달라지는 것은 dy/dz 뿐이므로,
dy/dz에 대해 자세히 알고 싶다면,


이고,
이를 다시 델타 규칙에 적용하면

이와 같다.
2.5 역전파 알고리즘(Backpropagation Algorithm)
경사 하강법엔 문제점이 있다.
다층 신경망을 학습시키는 경우 모든 노드에 식이 연결되어 있는데, 이를 미분하는데 엄청나게 오랜 시간이 걸린다

실제로 이 한계로 인해 오랜 기간 동안 신경망이 발전하지 못했다.
그러다가 1986년도에 데이비드 등에 의해 오차 역전 파란 방법을 개발되는데 이는,
마지막 노드인 출력 노드에서 한 번만 미분한 뒤 , 그 결과를 뒤의 노드에 전달하면서 재사용하는 방법이다. (동적 계획법?)

이로 인해 빠른 학습이 가능해졌고, 신경망이 다시 주목받기 시작했다.
위의 예시로 역전파가 출력층에서 거꾸로 아래로 내려가며 계산하는 방식임을 알았다
그러면 먼저, 역전파의 반대인 순 전파에 대해 알아보겠다
순 전파

앞에서부터 뒤로 순차적으로 진행됨
각 계산 과정마다 오차가 발생하는데, 각 노드 중 오차가 크게 발생한 요인들의 값을 큰 폭으로 변화시켜
오차의 값을 줄여나감 // 오차 역전 파도 이런 로직을 실행하지만 수치 미분을 사용하지 않아 더 효율적인 미분이 가능(?)
(오차 역전파 전까지 ) 지금까지는 수치 미분이라는 방법을 사용
순 전파 vs 역전파
순 전파와 역전파를 간단한 예로 비교하여 설명하면 이러하다.
<순 전파 : input -> Output>
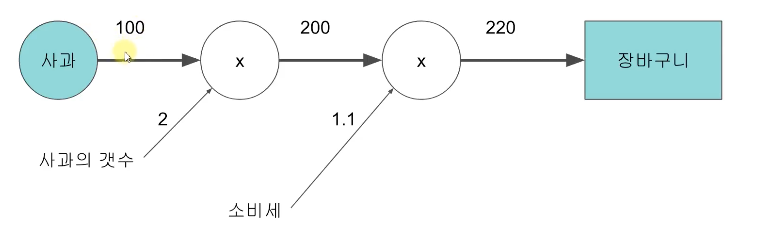
사과의 가격을 Input으로 하여, 장바구니에 담길 때 사과의 최종 가격을 계산하는 (유사..) 신경망이다
<역전파 : Output ->Input >

역전파의 Final Output인 2.2는 기울기(그래디언트)라고 볼 수 있다.
학습망의 최초 Input(100)을 X라고 하고,
학습망의 최종 Ouput(220)을 Y라고 하자.
그럼 X(사과의 값)가 얼마나 변화하던 Y의 값은 X * 2.2로 동일하다
이제 책에 나온 예제를 통해 알아보자
역전파 알고리즘에서 Hidden Layer의 노드들이 무엇을 해야 하는지는 알지 못한다.
하지만 Hidden Layer의 활성도(출력 값 y)를 바꿀 때 얼마나 빨리 오차가 변하는지(오차의 변화량 = 오차의 도함수 dE/dy)는 계산할 수 있다.
이를 통해 개별 연결의 가중치(w)를 바꿀 때 오차가 얼마나 빨리 변하는지(오차의 도함수 dE/dw)를 알 수 있다.
궁극적으로는 (오차 함수에서) 가장 가파른 하강 방향을 찾으려고 하는 것인데 = (오차 함수에서 하강 방향) 경사가 가파른 곳 = (오차 함수에서 하강 방향) 그래디언트 값이 큰 곳
2.3에서 델타 규칙 부분을 보면 그래디언트(오차 함수의 경사) 값은 dE/dw였다

결국 , 그래디언트 dE/dw가 가장 큰 값을 찾으려는 것이다. 그러니 가중치를 바꿀 때의 오차의 변화량(dE/dw)을 찾는 것이 의미가 있는 것
각 Hidden Layer(은닉층)의 노드는 많은 (Output) 출력 노드에 영향을 미친다. (계산이 많이 필요하다는 뜻)
그렇기 때문에 효율적인 방법으로 각각의 노드에서 발생하는 오차를 조합해야만 한다.
이를 역전파 알고리즘에선 동적 계획법(Dynamic programming)을 이용하여 조합한다.
+추가)
<동적 계획법>
자세한 건 컴퓨터 알고리즘
Hidden Layer에서 한 개의 층(k)에 대한 오차 도함수(dEk/dY)를 얻고,
이를 이용해 해당층 바로 아래층에 대한 오차 도함수(Ek-1/dW)를 구하는 데 사용한다.

위의 목표를 어떻게 달성하느냐?
이는 k층에 대한 오차 도함수(dE^(k)/dY)를 아래층(k-1)의 활성도(Y k-1)*에 대한 오차 도함수(dE/dYk-1 == dE/dXk)를 계산하는 데 사용한 후,
*아래층의 활성도는 위층의 input값과 같다 / 즉, Yk-1 = Xk
은닉 노드의 활성도에 대한 오차 도함수(dE/dYk-1 == dE/dXk)를 이용하면,
은닉 유닛들로 이어지는 가중치에 대한 오차 도함수(dE/dWij)를 구하기 매우 쉬워진다.
이제 한번 위의 방법을 통해 구해보도록 하자.
가장 위인 출력층으로 오차 도함수로부터 그 아래층의 가중치에 대한 오차 도함수를 구해보자
목표를 그림으로 나타내면 다음과 같다

이제 과정을 보면,

결과 적으로 다음과 같은 결과를 얻게 된다.

결국, 이 알고리즘을 완성하기 위해 이전과 마찬가지로 데이터셋에 전체 학습 예제에 대한 편도 함수를 합산한다.
(2.3의 델타 규칙에 대입하면 다음과 같은 식을 얻을 수 있다.)


(Wij니까 행렬임)
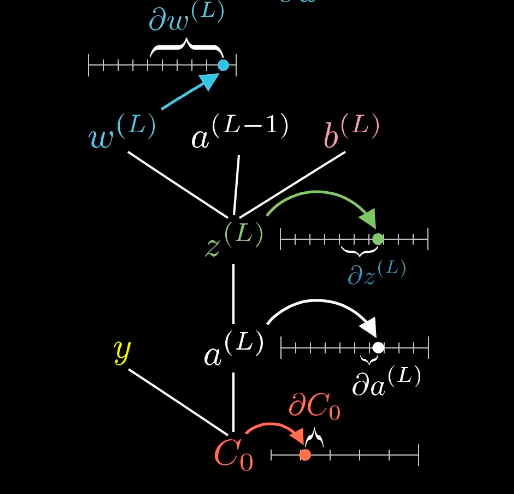
a(L - 1) : L-1층에서 계산되어 나온 예상값 y-hat, 즉, l층에 input값 x임
즉 z = w x(l-1층) + b
f(z) = a^L (L층에서 계산되어 나온 예상값 y-hat)
C는 오차함수 (a^L - y(실제 정답값))
오차함수는 a^L의 변화에 영향을 받고, a^L은 z의 변화에 영향을 받고, z는 w,a,b의 변화에 영향을 받는다
즉, W의 변화는 w에 대한 z의 변화량(dz/dw) , z에 대한 a^L의 변화랑(dy/dz), 오차함수에 대한 a^L변화량(dE/dy)을 유발하고
결국 오차함수를 변화시킨다.
이 식은 2.4에서 이미 계산한 값이며, 우리는 다양한 변화중에 w를 변화시켜 오차함수를 최소화 하는 방법을 사용하므로 위와 같은 방법을 사용했고 dz/dw = a^(L-1)즉 해당 뉴런으로 들어오는 input값 x이며, 전 단계 계층에서 계산되어 나온 결과이다.
즉 w의 변화량이 얼마나 오차함수를 변화시킬지는 이전 계층이 얼마나 큰 값으로 y(이전 노드의 활성화 정도)를 가지는 지에 달려있다.
즉, 이전 계층의 해당 노드의 연산 결과가 크게 나올 수록 w를 변화시켰을때 오차함수를 변화시키는데 더 큰 기여를 한다는 의미
www.youtube.com/watch?v=tIeHLnjs5U8&t=4s
당연히 위에 따르면 오차함수를 변화시킬 수 있는 값은 w,a,b 3가지가 있다.
a는 우리가 변화시키기 어려운 값이므로 w, b를 변화시키는데
위는 w에 대한 변화량만을 계산한 것이고 b도 마찬가지로 계산해주어야 한다.

dC/dw의 식을 dC/db로 변경해 주기만 하면되는데
dz/db = 1이므로 dC/dw의 계산을 가져다 쓰면 계산이 쉬워진다
2.6 확률적 경사 하강법(stochastic gradient descent)과 미니 배치 경사 하강법(mini-batch gradient descent)
2.5의 예제 알고리즘은 배치 경사 하강법(batch gradient descent)이라는 경사 하강법(gradient descent)의 한 버전을 사용한 것이다.
배치 경사 하강법(batch gradient descent)
배치 경사 하강법의 기본 개념은 전체 데이터셋을 사용해 오차 곡면을 계산한 후 경사를 따라 가장 가파른 하강 경로를 취하는 것이다.
오차 함수가 계속 설명한 w1, w2만을 가지는 이차 함수 (이차 오차 곡면) 일 때는 이것이 잘 작동하지만,
대부분의 오차 곡면은 훨씬 더 복잡할 수 있다.
예를 들어보면, 다음 그림과 같은 오차 함수가 있다고 하자

지금 까지 배운 배치 경사 하강법을 사용하면, 평평한 구간(미분 값이 찾아서 갈 텐데,
만약 평평한 면이 제일 낮은 지점이 최솟값을 가지는 지점이 아니라면?? 경사 하강법을 수행하다가 구간 내에 갇혀버릴 수 있다.
이게 바로 안장점(saddle point)인데... 안장점에 대해 설명하지 않으려고 했으나 결국 나오고 말았다... 위의 최대 최소를 설명한 접혀있는 더보기를 보고 오길 바란다...
이변수 함수에서 fx(a, b)=fy(a, b)=0을 가지는 점은 //x, y로 값입니다.
임계점, 안장점 두 개가 있는데
임계점은
1) fx(a, b) = fy(a, b) = 0 OR 2) (a, b)에서 fx나 fy가 존재하지 않는 경우이다.
안장점은
함수 f(x, y)가 = fy(a, b)=0일 때,
(a, b)의 임의의 근방에 f(a, b)>f(P), f(a, b)<f(Q) 만족하는 점 P, Q가 모두 존재하면(극대도 극소도 아니므로 극값이 아님)
f는 (a, b)에서 안장점 (a, b, f(a, b))를 갖는다고 한다.
대표적 예시로 이해를 도우면, 쌍곡 포물면의 안장점을 들 수 가있다.

*일변수 함수에서의 극대, 극소
[ 어떤 열린 구간 I에 속하는 모든 x에 대하여, f(a)>=f(x)가 성립하면, f(a)는 f의 극대 값
f(a)<=f(x)가 성립하면, f(a)는 f의 극소값이라고 한다. ]
다음의 방법을 사용하면 평평한 구간을 탐색하는 능력이 크게 향상된다
확률적 경사 하강법(Stochastic gradient descent)
확률적 경사 하강법은 각 반복에서 오차 곡면 이단일 예제에 대해서만 추정된다.
이렇게 되면 배치 오차 곡면에 따라 변동하기 때문에(동적 오차 곡면) 안장점을 회피할 수 있어,
확률적 곡면상에서 하강하는 것은 평평한 구간을 탐색하는 능력을 크게 향상할 수 있다.

그러나 확률 경사 하강법은
한 번에 한 가지 예에서 발생한 오차를 보는 것이라 오차 곡면에 대한 충분히 좋은 근사가 아닐 수 있다는 단점이 있다.
이런 이유로 경사 하강법 계산에 상당한 시간이 소요된다.
이 문제를 해결할 방법은 다음과 같다 -> 하나의 데이터도 아니고 전체도 아닌 부분집합으로 탐색을 하기
미니 배치 경사 하강법(mini-batch gradient descent)
미니 배치 경사 하강법은 반복마다 전체 데이터셋의 부분집합에 대해 오차 곡면을 계산한다.
이 부분집합을 미니 배치(mini batch)라고 하며,
미니 배치의 크기는 학습률과 함께 또 다른 하이퍼 파라미터가 된다.
미니 배치를 정하는 것은 경사 하강법의 효율성과 확률적 경사 하강법에 의해 제공된 지역 최솟값 회피(local minima avoidance) 사이에서 균형을 유지한다.
역전파와 관하여 가중치를 갱신하면 다음과 같다.
거의 같지만 다른 점은 dataset을 mini batch안의 예제들만 합산한다는 것이다.

2.7 데스트 데이터(Test Set)와 검증 데이터(Validation Sets) 그리고 과적합(Overfitting)
인공 신경망의 주요 문제 중 하나는 모델이 너무 복잡하다는 것이다.
계층도 많고, 계층당 노드(뉴런) 수도 많고, 이들의 연결도 많고, 파라미터도 많고... 등등 매우 복잡하다.
이것은 큰 문제이다.
예를 들어 설명하면,
input 데이터 x에 대해 output 데이터 y를 예측하는 모델을 개발하려고 한다.
다음 그래프에 점들은 학습 데이터의 실제 예제이고,
곡선(12차 다항식)과 직선(선형)의 두 가지 학습된 모델이 있다.

22 <12차 다항식 모델>
- 모든 데이터 x에 대해, y를 정확히 예측함
- 매우 인위적이고 복잡함
<선형 모델>
- 데이터 x에 대해, 근접한 y값을 예측함
- 인위적이지 않고, 간단함
두 가지 중 어떤 모델이 더 신뢰(trust)가 가는가? 선형 모델이다.
왜 선형 모델인지 모르겠다면, 학습 데이터(점 x로 표기되어있다)를 조금 더 추가해보자.

<12차 다항식 모델>
- 일부 데이터 x에 대해, 예측한 y의 오차가 매우 큼
- 매우 인위적이고 복잡함
<선형 모델>
- 모든 데이터 x에 대해, 근접한 y값을 예측함
- 인위적이지 않고, 간단함
이제 확실히 위의 예시에서는 12차 다항식 모델보다 선형 모델이 더 신뢰가 간다는 것을 알 수 있을 것이다.
데이터가 많아질수록 이 사실을 더욱 확인하기 쉬울 것이다.
과적합
위의 예제를 통해 알 수 있다시피,
12차 다항식 모델처럼 아주 복잡한 모델을 만들면 학습 데이터셋에 완벽하게 맞추기가 쉽다.
학습 데이터와 모델을 일치시키기 위하여, 일반적인 모양이 아닌, 곡선 자체를 뒤트는 등의 큰 자유도를 주었기 때문이다.
그러나 이렇게 될 경우, 새로운 데이터 셋을 판정하면 매우 오차가 커진다.
일반화를 제대로 하지 못한 것이다
이런 현상을 과적합이라고 한다.
과적합을 발생시키는 두 가지 요소
1. Hidden Layer의 노드(뉴런) 수가 많아질수록 과적합

위의 그림은 각각
두 개의 입력과 두 가지 크기의 소프트 맥스 출력, 3, 6, 20개의 뉴런을 가진 Hidden Layer로 구성된 신경망이다
뉴런의 수가 많아져 망의 연결 수가 증가할수록 데이터에 지나치게 과적합 하는 경향이 있다는 것을 보여준다.
2. Hidden Layer의 수가 많아질수록 과적합

위의 그림은 각각
3개의 뉴런으로 된 은닉층이 1, 2, 4개씩 있는 신경망을 사용한 결과를 시각화한 것이다.
층에 개수가 많을수록 데이터에 지나치게 과적합 하는 경향이 있다는 것을 보여준다.
위의 내용으로 3가지 결론을 얻을 수 있다.
<과적합을 막는 이론적 결론>
1. 모델은 항상 모델의 복잡성과 과적합 사이의 trade-off*를 고려해야 한다
trade-off : 두 개의 정책목표 가운데 하나를 달성하려고 하면 다른 목표의 달성이 늦어지거나 희생되는 경우의 양자 간의 관계.
모델이 복잡해지면 과적 합의 위험을 감수해야 하고,
모델이 충분히 복잡하지 않으면 문제를 해결하도록 학습할 만큼 강력하지 않을 수 있다.
특히 사용할 수 있는 데이터양이 제한된 경우 더욱더 과적합에 유의해야 한다.
딥러닝은 아주 복잡한 모델을 다루고, 복잡한 문제를 풀기 때문에 , 과적합 방지를 위한 대책을 적용하여 접근해야 한다.
(층당 뉴런의 수와 층의 갯수를 조절해야함)
2. 학습 데이터(Training set)와 테스트 데이터(Test set)를 나누어야 한다
학습에 사용한 데이터를 이용하여 모델을 평가하는 것은 큰 오류의 소지가 있다.
마치 시험문제에 교수님이 작년 문제를 그대로 똑같이(학습 데이터를 테스트 데이터로 활용할 경우) 내면 학생이 얼마나 해당 단원을 잘 이해했는지 알 수 없기 때문에, 다른 문제를 출제(학습 데이터와 테스트 데이터를 따로 둔 경우)하는 것과 비슷하다..
예를 들어 위의 그림을 다시 가져와보면

그래프 위의 점으로 찍힌 예제들만으로
모델을 평가한다고 하면,
12차 다항식 그래프는 선형 모델보다 적합하다는 결과를 도출하게 된다.
이는 거짓이므로,
학습에 사용되는 데이터(Training set)와 모델을 평가하는 데이터(Test set)를 분류해서 사용해야 한다
아직 학습할 때 보지 못한 새로운 데이터를 얼마나 잘 일반화하는지 측정하는 것이다.

실제 많은 상황에서 대규모 데이터 셋을 구하기란 매우 어렵기 때문에, 학습과정에서 모든 데이터를 마음대로 전부 사용해서는 안된다.
3. 과적합되는 시점을 찾아 과적합이 시작되자마자 학습을 멈추자 (검증 데이터 (Validation data) 이용)
데이터를 학습시키다보면 어느 순간까지는 유용한 특징들을 학습해서 모델을 구성하지만
어느순간이지나면 오히려 학습 데이터에 맞춰 그래프가 과적합되기 시작한다
그 순간을 알아내 과적합이 시작되자마자 학습을 종료하면 좋은 모델을 만들 수 있을 것이다

이를 위해 학습 과정을 에포크(Epoch)라는 단위로 나눈다
한 에포크는 학습 데이터 전체에 대한 한 번의 반복 과정이다.
즉 , 학습 데이터의 크기가 d이고, 미니 배치 경사 하강법의 배치 크기가 b이면, 한 에포크는 d/b번의 모델 갱신과 같다.
검증 데이터
한 에포크의 끝에서 모델이 얼마나 잘 일반화됐는지를 "검증 데이터(Validation data)"를 이용해서 평가한다.
<검증 데이터의 이용>
1) 과적합 시기 판정
검증 데이터로 평가한 모델의 정확도가 동일하거나 줄어들고 있는데,
학습 데이터의 정확도는 계속 증가한다면, 학습 데이터에 맞추어 모델이 과적합 되고 있다는 의미 이므로 학습을 멈춰야 한다.

2) 하이퍼 파라미터 최적화
하이퍼 파라미터 최적화 과정에서 정확도의 대리 측정(Proxy measure)에 이용한다
격자 탐색(Grid search) 방법을 이용한다.
하이퍼 파라미터에 대해 정해진 선택지 집합에서 하나의 값을 고른 후, 해당 하이퍼 파라미터(학습률의 집합/배치 크기의 집합)들의 모든 가능한 조합으로 모델을 학습시킨다.
검증 데이터에 대해서 최적 성능을 보이는 하이퍼 파라미터를 선택한다

최적의 조합으로 학습되었고, 과적합이 시작될 때 학습을 막아 생성된 최적 모델은 테스트 데이터를 통해 학습된 모델의 정확도를 확인한다.
(최종 1회)
<데이터를 나눌 때 주의할 점>
마지막에 1회만 테스트 데이터를 통한 검증이 시행되므로, 테스트 데이터 셋은 미지의 데이터를 잘 대변할 수 있도록 선정해야 한다.
검증 데이터는 여러 번 시행될 수 있지만, 테스트 데이터 셋을 잘 대변해야 한다.
<신경망 학습 파이프라인>

2.8 신경망에서 과적합(Overfitting) 막기
과적합을 막기 위해 제안된 몇 가지 기술이 있는데,
그중 하나는 정형화(정규화/Regularization)이다
정형화에 대해 설명하기 전에
좋은 모델은 어떤 기준으로 평가될까? 위의 파이프라인에서도 봤듯이
- 현재 데이터(training data)를 잘 설명하는가
이미 학습한 데이터에 대해 잘 작동하는가? = 학습 데이터에 대해 오차가 적다
- 미래 데이터(Test data)를 잘 예측하는가
테스트 데이터에 대해 잘 작동하는가? = 테스트 데이터에 대해 오차가 적다.

Training set에 대한 MSE(Mean squared Error : 평균 제곱 오차)를 최소화하면, 현재 데이터를 잘 설명하는 모델일 것이고,
Test set에 대한 MSE를 최소화한다면, 미래 데이터를 잘 예측하는 모델일 것이다.
먼저, Training set에 대한 예상 MSE를 분석해보면,

다음과 같이 3 부분으로 나누어지는데, 우리가 손쓸 수 없는(모델로 해결 불가능한) Irreducible Error를 제외하면,
우리는 Bias^2와 Variance를 최소화함으로써, 최소 MSE를 만들어 낼 수 있을 것이다.
+ Bias와 Variance
Bias : 편향 목표지점에서부터 얼마나 치우쳐있는가
Variance : 목표지점에서 얼마나 흩어져있는가

우리가 가장 원하는 답은 2번 Low Variance / Low Bias이지만,
상황에 따라 한 가지를 포기하더라도 최악(3번)은 면하도록 해야 할 것이다.
즉, Bias가 증가되더라도(안 좋아짐) variance감소폭이 더 크다면 expected MSE는 감소할 것이고,
미래에 대한 예측 성능이 좋아질 것이다
어떻게 MSE를 줄일 수 있을까? 가장 잘 알려진 방법은
"최소 제곱법(Least squres method)"라는 것이다.
MSE를 최소화 하는 회기계수(B =(B1, ... ,Bp)베타 벡터)를 계산해주는 식이구나 정도로 알면된다
최소 제곱법으로 베타벡터를 구하면 다음과 같다.

하지만 이 방법으로 얻어진 베타벡터(점들의 추정량)는 unbiased한 상태에서의 분산이 가장 작은 점들의 추정량이다.
편향이 전혀없는 상태에서 분산이 가장 적은 상태이니 아주 좋을 수 밖에 없다.
하지만, 여기서 생기는 의문은 위에서와 마찬가지로
조금 Bias가 커지더라도 Variance를 줄이는게 더 이득일 수 있지 않을까? 하는 의문이다.
여기까지 이해했다면 정규화Regularization에 대해 들을 준비가 되었다
그래도 조금만 최소제곱법을 더 알아보자면,
최소제곱법은 흩뿌려진 자료들의 일관성을 찾기위해, 이 자료들의 오차가 최소가 되는 함수 f(x)를 도출하는 방법이다.
여기서 f(x)는 일차함수라고 가정한다.

식을 보면 이러하다,
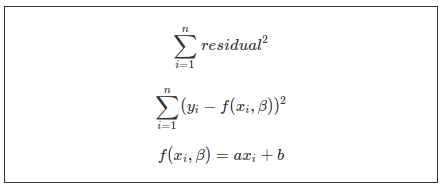
이정도로 알아두고 다음으로 넘어가자
선형결합이 문제점의출발???
정규화(Regularization)
다음 그림을 참고하자

그림을 보면, 과적합 상태를 적절한 상태로 돌리고 싶으면 B3, B4를 0에 가깝게 만들어 x^3과 x^4항을 제거하면 된다.
이와 같은 원리를 에러함수에 적용시켜보면
에러 함수에 특정 식을 더하거나 빼는 등의 연산을 통해 에러함수의 모양을 변경할 수 있다는 말이 된다.
정형화는 큰 가중치의 값들을 불리하게 하는 부가적인 항을 추가해 최소화하는 목적 함수를 수정함으로서 진행한다.

부가적인 항의 크기에 따라, 얼마나 제약을 둘지가 결정되고 그에따라 그래프의 모양이 달라진다


λ이 매우 큰 값을 가질 때는
모델이 학습 데이터에 대해 좋은 성능을 내는 것보다는 세타를 가능한한 작게 유지하는 것이 중요하다는 것이다.
λ값의 결정은 매우 중요하며 시행착오가 필요 할 수 있다.
대표적인 정형화의 방법에는 3가지(L2 정형화, L1 정형화, 드롭아웃)이 있다.
L2정형화(L2 Regularization or Rdige)
신경망에서 모든 가중치의 제곱의 크기로 오차함수를 증가시킴
이는 신경망의 모든 가중치 w에 대하여, 오차함수 E에 1/2*λ*w^2항을 추가하는 것이다
즉, 다음과 같다.

주로 제일 많이 사용하는 정형화 방법이다.
이 정형화의 특징은
최고점인 가중치 벡터의 영향력을 줄이고 분산된 가중치 벡터들을 선호하는 직관적 해석
신경망입력중 일부를 많이 사용하지 않고, 모든 입력을 조금씩 사용하게 유도
경사 하강법 갱신동안 모든 가중치가 선형적으로 0으로 감소 (-> L2 정형화를 가중치 감쇠(weight decay) 라고도 함)
예시)
2개의 입력 / 크기가 2인 소프트맥스 층 / 20개의 뉴런
배치크기 10인 미니배치 경사 하강법
λ(정형화 강도) 각각 0.01 , 0.1 , 1

L1정형화(L1 Regularization or Lasso)
신경망의 모든 가중치 w에 대해 절댓값을 취한다

특징
최적화 하는 동안 가중치 벡터를 드문드문하게 만든다
즉, 가장 중요한 입력의 작은 부분 집합만을 사용하게 되고 입력 노이즈를 매우 잘 견디게 된다.(L2정형화와 반대)
어떤 특징들이 판정에 기여하고 있는지를 정확히 이해하고자 할 때
이런 특징 분석 수준이 필요 없다면 경험적으로 L2정형화가 더 잘 수행됨
최대 놈 조건(max norm constraint)
파라미터(θ or w)가 매우 커지는 것을 직접적으로 제한하는 목적
모든 뉴런에 대해 입력 가중치 벡터 크기의 절대 상한선을 적용한 후, 제약조건을 강제 도입하기 위해 Projected(투영된) 경사하강법을 사용
놈(norm) - feat. 선형대수학
: 벡터의 크기 또는 길이를 측정하는 방법
x과 다음과 같을 때,

1) L1 norm 맨해튼 놈
벡터의 모든 성분의 절댓값을 더한값

2). L2 norm 유클리드 놈
벡터의 모든 성분을 제곱하여 더한값의 루트값 (직선거리)

다음과 같이 경사하강법 단계에서 입력 가중 벡터를 중심이 원점이고, 반지름이 c인 구 위에 투영한다(c는 주로 3,4를 사용)

특징
가중치 갱신이 항상 제한되어 가중치 벡터가 통제 불능상태(학습률이 너무 높더라도)가 되지 않음
드롭아웃(drop out)
과적합을 막기위한 방법중 하나(특히 심층 신경망에서 주로 사용)
어떤 확률p(하이퍼파라미터, 해당 뉴런이 존재할 확률)로 뉴런의 활성 상태를 유지(1, 즉 출력값이 변동없이 계산된 값 그대로 출력)하거나 0(비활성화 , 즉, 출력값이 0임)으로 설정하여 구현.

이러한 방식으로 기하급수적으로 많은 다른 신경망 구조를 간략하게 결합하는 방법을 제공하여 과적합을 방지함
특징
특정 정보가 없을 때도 망을 정확하게 만들게 하고, 망의 뉴런의 어느 하나나 매우 적은 조합에 너무 의존적이 되는 것을 방지한다.
고려해야할 점
만약 p = 0.5라고 가정하고, 모든 뉴런이 정확히 0.5의 확률로
예를들어 6개의 뉴런이 있을때, 3개는 비활성화되었고, 3개는 활성화 상태로 남아있다고 가정하자
(출력값을 x라고 가정하면,) 그렇게되면 오차함수 E = 0.5 * x + (1 - 0.5) * 0 = 0.5*x가 될 것이다
비활성화 된 뉴런들의 값
활성화된 뉴런들의 값 (비활성화 되어야 하기 때문에 0을 곱해줌)
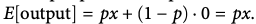
하지만, 학습이 아닌 테스트 시(2.7참고) 에 뉴런이 출력될 때 크기 조정이 필요하므로 일반적인 드롭아웃을 적용하는 것이 바람직 하지 않다.
테스트에 걸리는 시간은 모델의 최종 평가이므로 매우 중요하다.
따라서 테스트 시간 대신 학습 시간에만 p를 조정해주는 역드롭아웃을 사용하는 것이좋다.
역드롭아웃에서 비활성화되지 않은 뉴런(드롭아웃되지 않은 뉴런)은 값이 다음층으로 전파되기 전에 p의 확률로 나눈 출력을 갖게 되므로

테스트 시 뉴런의 출력 크기를 임의로 조정하는 것을 피할 수 있다.
tf.nn.dropout(hidden,p)으로 사용가능한데, 학습시에만 p를 이용하여 dropout(0.5~0.7권장)하고, 테스트 시에는 p = 1(dropout없이)로 설정해주어 검사한다.
이게 찾아봐도 정확히 안나오는데 이 함수를 수행하면 역드롭아웃이 수행되는 것으로 ..? 생각됩니다.
<참고자료>
딥러닝의 정석 - 니킬 부두 마
www.youtube.com/watch?v=xgT9xp977EI
www.youtube.com/watch?v=Ei_md7n40mA
www.youtube.com/watch?v=0DUIVcpTpT
www.youtube.com/watch?v=GtLe9Z2No28
https://www.youtube.com/watch?v=pJCcGK5omhE
L1, L2 Regularization (Lasso, Ridge)
머신러닝을 위한 파이썬 워밍업에서 Linear Regression 파트를 공부하며 복습한 내용을 적어본다. Overfitting 의 문제 Regularization 이라는 문제에 앞서 항상 먼저 나오는게 overfitting 이슈다. 기술 관련 이
dailyheumsi.tistory.com
https://www.youtube.com/watch?v=IHZwWFHWa-w
<추천영상 : 이 영상 교수님이 추천해주신건데 진짜 좋아요>
딥러닝 용어 정리, L1 Regularization, L2 Regularization 의 이해, 용도와 차이 설명
제가 공부하고 정리한 것을 나중에 다시 보기 위해 적는 글입니다. 제가 잘못 설명한 내용이 있다면 알려주시길 부탁드립니다. 사용된 이미지들의 출처는 본문에 링크로 나와 있거나 글의 가장
light-tree.tistory.com
dailyheumsi.tistory.com/57?category=830870
L1, L2 Regularization (Lasso, Ridge)
머신러닝을 위한 파이썬 워밍업에서 Linear Regression 파트를 공부하며 복습한 내용을 적어본다. Overfitting 의 문제 Regularization 이라는 문제에 앞서 항상 먼저 나오는게 overfitting 이슈다. 기술 관련 이
dailyheumsi.tistory.com
[선형대수학] 놈(norm)이란 무엇인가?
오늘은 놈(norm)에 대해 설명을 드리고자 합니다. 놈은 노름으로 발음하기도 하는데 둘다 어감이 좀 그렇죠? 선형대수학에서 놈은 벡터의 크기(magnitude) 또는 길이(length)를 측정하는 방법을 의미합
bskyvision.com
'ML' 카테고리의 다른 글
| [딥러닝의 정석] 05. 합성곱 신경망-1 (0) | 2020.08.02 |
|---|---|
| [딥러닝의 정석] 04. 경사 하강법을 넘어서 (0) | 2020.07.27 |
| [딥러닝의 정석]03. 텐서플로로 신경망 구현하기-2 (0) | 2020.07.21 |
| [딥러닝의 정석]03. 텐서플로로 신경망 구현하기 (0) | 2020.07.18 |
| [딥러닝의 정석] 01. 신경망 (0) | 2020.07.06 |



