제목이 마음에 안 드네요 근데 이제 와서 단원명으로 제목을 안지을 수도 없고..
4.11 요약
- 복잡한 오차 곡면이 있는 심층 신경망을 학습시킬 때의 문제 : 가짜 지역 최솟값 문제 (2단원 경사 하강법 문제)
- 안장점과 기타 나쁜조건이 미니 배치 하강법에 얼마나 악영향을 주는지
- 나쁜 조건 극복(모멘텀
- 헤시안 행렬
- 더 나은 수렴을 위한 학습률 조정법
4.1 경사 하강법의 과제
심층 신경망을 끝에서 끝까지 학습시키기려면
방대하게 분류된 데이터셋
향상된 하드웨어( GPU? )
여러 가지 알고리즘 적 발견 ( 활성화 함수 등 )
기타 등등
의 여러 가지 분야에서 기술혁신이 요구된다
오랫동안 딥러닝 모델로 표현되는 복잡한 오차 곡면을 극복하기 위해 Greedy layer - wise training 방법에 의존했다
탐욕적 층별 학습(Greedy layer - wise training)
2006년 이전에는 hidden layer가 2개 이상이 되는 네트워크를 학습시킬 방법이 별로 없었다.
(Vanishing/Exploding gradient와 Overfitting 문제 등등)
Vanishing / Exploding gradient problem
쉽게 말하면 neural network의 가 계속 전파되면서 초기의 weight를 잊어버리거나(기울기(gradient)가 0에 수렴), 무한히 커지는 현상을 의미
깊게 들어가 보면 이는 활성화 함수 f(z)와 관계가 있는데
활성화 함수가 어떻게 gradient를 0이나 무한대로 만드나? : 의문을 해결하려면 여기에 대해 논해야 하지만,
그거보다 더 먼저 활성화 함수가 gradient관계가 있었나?(있으니까 값을 바꾸는데 기여할 것임)부터 설명해야겠다 왜냐면 내가 까먹음.. 이미 알고 있다면 스크롤을 좀 내려서 아래부터 봐보자
2단원에 대한 quick, simple 부분적 review가 될 것~
하나의 뉴런으로 우리가 지금까지 배운 것을 간략화해보면 이렇다 (bais생략)

우리는 이 뉴런에서 계산된 우리의 y를 더 좋은 값으로 만들고 싶다
그러기 위해 우리는 오차 함수(E)라는 것을 만들어냈는데,
기본적으로 오차라는 것은 E = 정확한 값 - 예상 값 = t - y인데요, 이를 신경망에 더 맞는 방식인 방법으로 조금씩 개량해서 오차 함수로 사용한다.
대표적으로 사용하는 오차 함수에는 MSE , CEE가 있습니다.(3단원 -2 게시글 참고)

y는 이미 정해진 값이 아닌 위쪽의 뉴런 그림에서 보다시피(아래 다시 넣음)
여러 요소에 의해 변화하는 값이다(고정된 값이 아님)
그럼 지금까지 E는 y에 변화에 따라 변화한다고 결론을 내릴 수 있다.
y는 활성화 함수를 통해 나온 값이고, 활성화 함수에는 여러 가지가 있지만

y는 z를 입력값으로 받아 z의 값에 따라 y도 변화한다
그럼 z는 보다시피 w와 x에 따라 변화하는 값이고, (bias 일단 제외)
x는 이미 정해진 값이라고 했고, w가 갱신될 파라미터 즉 변수이니
결론적으로는 E라는 함수는 w에 의해 변경된다고 볼 수 있다 -> w를 줄이면 E를 줄일 수 있다는 결론에 도달
우리는 2단원에서 이런 E라는 함수를 잘 모르기 때문에 최소화할 때 경사 하강법이라는 방법을 사용하기로 했었고
경사 하강법은 우리가 여태까지 말했다시피 E를 최소화하기 위해 W를 변경하는 방법이다
2단원에서 경사 하강법을 수행하기 위한 델타 규칙이라는 것을 설명했는데
W를 변화시키는 것은 W의 변화량(ΔW)이라는 의미고 그것은 바로 Gradient경사였다.
ΔW를 구하는 델타 규칙에 대해 다시 가져와보면

여기서는 활성화 함수로 시그모이드 함수를 사용했고 시그모이드 함수의 z에 대한 편미분은 y(1-y) 임

여하튼 결과적으로는 결국 활성화 함수를 미분한 값이 Δw(gradient)를 구하는 데 사용된다.
1. 뉴런 하나에서 계산한 y 예측값의 오차를 줄이려고 함
2. 그를 위해 오차 함수를 만들어냈고 해당 오차 함수는 y값에 의해 변화함
3. y값은 z값에 의해 z는 w에 의해 변화함 -> 오차함수는 w에 의해 변화함
4. 오차 함수를 최소화하기 위해 gradient(w의 변화량)을 이용함
5. gradient는 델타 규칙에 의하면 활성화 함수를 미분한 값에 의해 변화함
활성화 함수가 gradient관계가 있었나? 이에 대한 의문이 해결되었다
활성화 함수를 미분한 값은 gradient의 값에 영향을 준다
이제 이 질문에 답할 수 있게 되었다.
활성화 함수가 어떻게 gradient를 0이나 무한대로 만드나?
활성화 함수를 미분한 값이 0이면 gradient도 0으로, 무한대로 하면 gradient로 무한대로 갈 것이다
과거에는 시그모이드 함수를 활성화 함수로 많이 사용하였는데,
시그모이드 함수의 예를 들어보자

초록색은 시그모이드 함수이고, 파란색은 이를 미분한 값이다
딱 봐도 0에 가까운 부분이 많아 보인다.
시그모이드 함수를 사용하면, 미분 값이 0에 가까운 부분이 여럿 존재하므로
결국 학습을 반복하다 보면 gradient(ΔW)가 0에 가까운 값이 곱해져 0에 가까워질 수 있다. ->미분 값을 이용하는 역전파 학습이 어려워지거나 학습시간이 매우 오래 걸리게 됨 (2단원 학습률 나오는 부분을 참고)
이게 바로 Vanishing gradient problem이 발생하는 예시이다.
(이거 때문에 ReLU함수가 사용되는데 이는 나중에.. 아마?)
좀 멀리 왔는데 그러하다
여하튼 인공신경망에서 Vanishing/Exploding gradient와 Overfitting 문제는 매우 치명적인 결함으로 지목되었다.
몇 개의 CNN을 제외하고는 학습이 불가능한 수준이었다고 한다.
그러다가 2006년 이후 몇몇 학자들에 의해 Greedy Layer-wise Training이라는 방식이 발견되었고, 드디어 hidden layer가 여러 개인 심층 네트워크 학습이 어느 정도 가능해졌다.
이 방법은 미니 배치 경사 하강법을 사용하기 전에 한층씩 w파라미터의 더 나은 초기값을 찾은 뒤 학습시키는 방법인데,
(초기값의 중요성에 대해서는 3단원 맨 마지막 부분에서 언급했다)
사실 이 방법에 대해 자세히 다룰 필요는 없어 보인다 여기서는 그저 이 방법이 사용되었었는데, 그러다가 요즘에 최적화 방법에 대한 돌파구가 마련이 되어서 이제 그 방법을 쓰고 그 돌파구에 대해 알아보는 단원이다.
그래도 이 방법이 어떤 건지는 알기 위해 간단히 조사했다.

그림에는 3개의 hidden layer가 존재한다.
이 layer들을 각각 개별로 greedy 하게 학습시키는 것이다.
첫 번째 계층을 구할 땐, 2,3번째 계층을 없는 것으로 치고 학습시켜 greedy한 값을 알아낸다.
2번째 계층을 구할땐 첫 번째 계층을 고정시키고, 3번째 계층이 없다고 가정한 후 학습시켜 greedy 한 파라미터를 알아낸다
3번째 계층은 1,2 계층을 고정시키고 학습시켜 greedy 한 파라미터를 알아낸다.
이런 식으로 학습시켜 초기값을 알아낸 후 미니 배 치경 사법을 이용하면, hidden layer가 여러 개 있어도 학습이 가능해진다.
하지만 이 방법은 매우 시간이 많이 소요된다(time intensive)
또한, 최근에 최적화 방법에 대한 돌파구(breakthroughs)들이 마련되면서 끝에서 끝까지(end to end fashion model) 모델을 직접 학습시키는 것이 가능해졌다.
4단원에서는 이러한 돌파구에 대해 알아본다
4.2 심층 신경망(Deep Networks)의 오차 곡면(Error Surface)에서 지역 최솟값(Local Minima)
지역 최솟값이 성공적인 심층 모델 학습을 얼마나 방해할까?
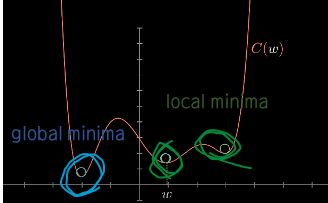
딥러닝 모델 최적화의 주요 과제는 오차 곡면의 전체적인 구조(global structure of the error surface)를 유추하는 것이다.
이를 유추하기 위해 최소한의 지역 정보를 이용하는데, 일반적으로 전체적인(global) 구조와 지역적인(local) 구조 사이에 유사성이 거의 없어 매우 어려운 문제다.
이는 다시 2단원에 제시한 문제로 돌아간다

어떤 사람(현재 파라미터 위치)이 그랜드 캐니언(오차 함수)의 어딘가에 매달려있다.
그는 그랜드 캐니언의 지반이 가장 낮은 곳(오차 함수의 최솟값)으로 가고 싶은데
그랜드캐니언의 전체 모습(오차 함수의 개형)이 어떤지도, 가장 낮은 곳(최솟값)이 어딘지도, 자신이 어디쯤 위치(현 파라미터의 위치)해있는지도 알지 못한다
그럼에도 지반이 가장 낮은 곳으로 가고 싶다면, 일단은 평평한 면을 만날 때까지 한발 한발 아래쪽의 경사를 따라 이동하는 수밖에 없다.
만약 그랜드 캐니언이 아래와 같이 지표면이 오목한 사발 모양( 수학적으로 볼록한 : convex라고 함)이라면

저 사람은 한 발 한 발아래로 내려가다 보면(경사 하강법), 가장 낮은 지점(global)에 도달할 수 있을 것이다
하지만 그랜드 캐니언은 절대 저렇게 단순하게 생기지 않았을 것이다
저 부분은 그랜드 캐니언의 아주 일부에 불과할 가능성이 크고, 훨씬 더 복잡하게 생겼을 것이다 (오차 함수도 마찬가지)

2장에서는 확률적 경사 하강법과 미니 배치 경사 하강법이 이러한 문제를 조금은 해결해 줄 수 있다는 것을 알았다.
하지만 이는 아래와 같은 얕은 지역 최솟값에 한한 이야기이다

이렇게 얕은 지역 최소에 대해서는, 다양한 데이터를 전체가 아닌 개별(확률적), 부분집합(미니 배치)으로 나눈 다양한 에러 함수를 살펴보면
얕은 곳이 local minima였다는 것을 알 수 있지만,
다음과 같은 깊은 지역 최소에 대해서는 개별, 부분집합으로 나눈 다양한 에러 함수도 모두 같은 부분을 minima로 가져 그곳이 local 했는지 알 수 없다.

이제 local minima가 심층 신경망에서 큰 문제가 된다는 것을 알았다.
그렇다면 실제 심층 신경망의 오차 곡선에서 지역 최솟값은 얼마나 일반적인가?
실제로 어떤 시나리오에서 학습상 문제가 발생할까?
4.3 모델 식별성(model identifiability)
모델 식별성이라는 개념에 대해 열심히 알아봤는데 통계 쪽 용어인 것 빼고 정말 정확히 무슨 뜻인지 알아내기가 너무 어려웠다
일단 알아는 봤는데 예측하면 이런 느낌 같음
모델 식별성(model identifiablitity)
식별 가능 identifiable
통계에서 식별 가능성은 정확한 추론이 가능하기 위해 모형(model)이 충족해야 하는 속성이다. 모형이 이론적으로 모형에서 무한한 수의 관측치를 얻어 모형의 파라미터가 참값으로 학습이 가능하다면, " 그 모형은 식별 가능하다(identifiable)"고 한다.
수학적으로 이것은 다음과 같다, 서로 다른 파라미터의 값이 관찰 가능한 서로 다른 확률분포에 의해 생성되어야만 한다
일반적으로 모델은 (식별 조건이라고 부르는 특정한 요구의 모음인) 기술적으로 제한된 특정 상황에서만 식별 가능(identifiable)하다.
정의

어떤 통계적 모델 P가 있는데, 해당 모델은 무한하거나 유한한 파라미터 차원을 가진다.
파라미터와 모델이 1대 1 관계를 이루면 해당 모델 P를 식별 가능하다고 한다.
파라미터 공간에 존재하는 모든 파라미터가 같으며 모델도 같음?, 즉 어떤 가능한 확률분포에 대해 하나의 모델을 가지고 있음?
모델 비 식별성(model non-identifiability) / 식별 불가능
식별 가능하지 않은 모델은 비 식별성( non-identifiable or unidentifiable) 모델이라고 부른다 : 2개 이상의 파라미터화(paramiterization)는 관찰적으로 동일하다. 모형이 식별 불가능한 경우에도 모델의 파라미터의 특정 부분집합 실제 값(참값)을 학습하는 것이 가능하다. 이런 경우 모델이 부분적으로 식별 가능(partially identifiable)하다 라고 한다. 다른 경우 매개변수 공간의 특정 유한 영역까지 실제 매개변수(참인 매개변수)의 위치(location)를 학습할 수 있으며, 이 경우 모델이 set identifiable 하다고 한다.
내 생각엔 딱 이 정도로 정리하면 될 것 같다. (정확히 맞는지는 잘..)
어떤 2개(그 이상) 모델들이 존재하는데, 이들은 서로 다른 파라미터를 가졌다? 그런데 모델들의 결과는 같아서? 두 모델을 non-identifiablity 한 성질을 가졌다.
en.wikipedia.org/wiki/Identifiability
Identifiability - Wikipedia
For a less technical treatment, see Parameter identification problem. In statistics, identifiability is a property which a model must satisfy in order for precise inference to be possible. A model is identifiable if it is theoretically possible to learn th
en.wikipedia.org
blog.naver.com/sw4r/221009113900
Nonidentifiability from Gaussian Errors (LiNGAM 관련 내용)
가우시안 에러를 가정해보자. 모델 1은 X1은 e1, X2는 0.8 x X1 + e2 이다. X <- BX + e 에서 B...
blog.naver.com
지역 최솟값의 근원은 모델 식별성(model identifiability)이라는 개념과 관련이 있다.
심층 신경망에 대해 알려진 점은 오차 곡면이 아주 많은 수의 지역 최솟값을 가지는 것이 확실하다는 것이다
크게 2가지 이유로 증명이 가능하다
1. 완전 연결 전방향 신경망의 한 층에서 뉴런들은 어떻게 재 정렬해도 여전히 신경망의 끝에서는 똑같은 최종 출력을 가짐 ( = 뉴런 재정렬의 대칭성)

결과적으로 n개의 뉴런으로 구성된 한 층 안에서 파라미터를 재배열하는 방법에는 n! 가지가 있다
그리고 각각 n개의 뉴런으로 구성된 l개층의 심층 신경망은 총 n!^(l) 개의 서로 다른 설정을 가진다.
하지만 이 모든 서로 다른 설정의 최종 출력 값은 같다.
2. ReLU뉴런의 경우 입력값에 상관없이 똑같은 최종 출력을 가짐
동일한 신경망에서 개별 ReLU뉴런 결과를 가지는 무한한 수의 동일한 구성이 있다고 하자.
ReLU는 조각마다 선형 함수를 사용하므로 신경망의 동작을 바꾸지 않고도 0이 아닌 상수 k를 들어오는 모든 가중치에 곱하고, 나가는 모든 가중치에 1/k을 곱함으로써 출력 값을 조정할 수 있다.
== 결과적으로 같은 최종 출력을 가지게 할 수 있다.
심층 신경망에서 위의 예시 둘 다 서로 다른 모델일지라도 같은 최종 출력을 가진다는 것은
심층 신경망이 비 식별적인 특성을 가진다는 뜻이다. ( non - identifiability )
이와 같은 이유로
오차 곡면이 아주 많은 수의 지역 최솟값을 가지는 것이 확실하지만, 궁극적으로 심층 신경망의 지역 최솟값들은 본질적으로 문제가 되지 않는다.
non identifiable 한 모든 구성이 제공되는 입력값과 상관없이 구별할 수 없는(non - identifiability)한 방식으로 작동된다.
이는 학습 데이터로부터 똑같이 배우고, 본 적 없는 예제들에 대해서도 일반화 과정을 통해 똑같이 작동한다는 의미로,
학습, 검증, 테스트 데이터 셋이 모두 동일한 오차를 발생시킨 다는 뜻이다.
사실 이게 정확히 무슨 뜻인지는 모르겠으나 내 예측으론 이렇다.
우리가 발생시킨 오차 함수가 다음과 같은 형태를 가지고 있고,
4개의 지역 최솟값이 있다고 해보자 (global 최소도 지역 최소에 포함됨)

이렇게 되어있을 때, 우리는 모든 다른 데이터셋의 학습에서 서로 다른 4개의 지역 최소로 도달할까봐 걱정하지 않아도 된다는 의미다.
학습은 2번 지역최소로 해놓고 검증이나 테스트 데이터 셋은 1번이나 4번을 찾아가지 않는다는 것이다.
학습을 2번으로 했다면, 테스트나 검증 데이터에 대해서도 2번 지역 최소를 구할 것이고
나머지 지역 최소에 대해서도 마찬가지이다. (즉 학습, 검증, 테스트 데이터 셋에서 모두 동일한 오차를 발생시킨다)
하지만 문제는 해당지역 최솟값이 진짜 global 한 최솟값이 아닐 때이다.
만약 아래 그림에서 1,2,3,4 총 4개의 지역 최소 중에 4번이 실제 전역 최솟값이라고 하자
근데 우리의 학습망은 1,2,3 중 하나로 학습을 진행한 경우, 우리의 학습망은 진정한 최소 값을 구할 수 없다.
이 1,2,3번 지역 최소를 가짜 지역 최솟값(spurious local minima)이라고 하며, 이들은 전역 최솟값(4번)의 가중치 구성보다 더 큰 오차를 발생시키는 신경망의 가중치 구성을 가진다.

이러한 종류의 가짜 지역 최솟값이 일반적이라면(많이 존재한다면) 경사 기반 최적화를 이용할 경우 지역 구조만 고려할 수 있기 때문에 최적화를 할 때 문제에 직면할 수 있다.(여하튼 최적 값 찾기 어렵다는 뜻)
4.4 심층 신경망에서 가짜 지역 최솟값(Spurious들은 얼마나 다루기 어려운가(Pesky)?
수년간 딥러닝 전문가들은 모든 문제가 가짜 지역 최솟값에서 심층 신경망을 학습시킨데에서 비롯된다고 생각했다.(정확한 근거는 없었음)
그러나 최근 많은 연구에서 지역 최소값 대부분이 전역 최솟값과 매우 유사한 오차율과 일반화 특성을 나타냄을 보여주고 있다.
(즉, 사실상 가짜 지역 최솟값은 그렇게 치명적인 문제가 아니라는 의미 , 가짜 지역 최솟값과 global최솟값이 별 차이가 없음)
이 문제를 단순화하는 방법의 하나는 심층 신경망이 학습할 때 오차 함수의 값을 시간에 대해 그리는 것이다.
그러나 이 전략은 오차 곡면이 울퉁불퉁한지(local minima가 다루기 어렵기 때문의 문제인지) 또는 나아갈 방향을 파악하는데 어려움이 있는지(평평한 면등등을 만나 어디로 나아갈지 결정이 어려운 문제인지)를 알 수 없어서 오차 곡면에 대한 충분한 정보를 주지 못한다
이 문제를 효과적으로 분석한 Goodfellow 등은 2014년에 두 잠재적 교란 요소(위의 두 문제)의 분리를 시도하는 한 논문을 발표했습니다.
시간에 대한 오차 함수를 분석하는 대신 선형 보간법(linear imterpolation)을 이용해
임의로 초기화된 파라미터 벡터(최초 초기값,θi)와 성공적 최종 해(최종 해θf) 사이의 오차 곡면(에러 함수 곡면)에서 어떤 일이 일어나는지를 조사한 것
선형 보간법

을 통해 모든 지점에서 오차 함수를 계산했다.
즉, 이는 1. 어느 방향으로 나아갈지 2. 지역 최솟값들이 경사 기반 탐색 방법을 방해하는지
두 가지를 조사한 것이다.
그 결과 이들은 다른 유형의 뉴런을 가진 실제 신경망의 매우 다양한 예시에도 불구하고,
파라미터 공간에서 임의로 초기화된 지점(최초 시작점)과 확률적 경사 하강법을 이용해 찾은 해 사이의 직접 경로는 다루기 어려운 지역 최솟값들로부터 영향을 받지 않는다는 것으로 보였다.
<결론>
즉, 사실 가짜 지역 최솟값은 심층 신경망 학습에 큰 문제가 되지 않는다(SGD를 사용하면).
2가지 문제 중 후자였던 지역 최솟값이 별로 큰 문제가 되지 않는 것을 알아냈으니, 진짜로 큰 해가 되는 것은 전자였던, 움직일 적절한 방향을 찾는 것이 어려움에 달려있다.
"Qualitatively characterizing neural netrwork optimization problems"라는 논문인데
Abstract 부분만 번역해봤습니다.
신경 네트워크를 교육하는 것은 대규모 비 볼록(non convex) 오차 함수를 최적화 문제를 해결하는 것을 포함합니다. 이 과제는 오랫동안 지역 최솟값이라는 매우 어려운 문제에 직면해 있다고 여겨져 왔습니다.
그러나 현대적인 신경망은 확률적 경사 하강법(SGD)을 이용한 직접적인 학습만을 통해 복잡한 과제에 대해 무시할 수 있을 정도의 에러율을 달성할 수 있습니다.
우리는 지역 최솟값을 극복하는 망을 증거로 제시하여 간단한 분석기술을 소개하려고 합니다.
사실, 우리는 초기값에서 solution값으로의 직선적인 경로를 찾아냈습니다.
다양한 상태(state)의 예술(art) 신경망은 절대로 어떠한 중요한 장애물도 마주치지 않습니다.
결론부터 말했지만 이는 우리가 3장에서 작성한 전방향 ReLU신경망을 통해 증명이 가능하다.
증명은 나중에 어쩌고...
4.5 오차 곡면의 평평한 구간
우리는 지금까지 local minima들이 별로 큰 문제가 되지 않는 것을 알게 되었다.
하지만 탐색을 방해하는 것은 local minima뿐만이 아니다.
중간중간에 위치해있는 gradient (경사)가 0인 부분(평평한 구간) 또한 학습을 방해한다.
이미 나온 개념인데 2.6 미니 배치/확률적 경사 하강법을 설명할 때 나온 임계점과 안장점들이다.

물론 이는 local minima때처럼 탈출할 수 없어 보이지는 않지만 학습 속도를 매우 저하시킨다.
2단원 글에 써놓았던 임계점과 안장점 개념을 다시 가져왔다.
더 자세하게 보려면 2단원 게시글 참고
이변수 함수에서 fx(a, b)=fy(a, b)=0을 가지는 점은 //x, y로 값입니다.
임계점, 안장점 두 개가 있는데
임계점은
1) fx(a, b) = fy(a, b) = 0 OR 2) (a, b)에서 fx나 fy가 존재하지 않는 경우이다.
안장점은
함수 f(x, y)가 = fy(a, b)=0일 때,
(a, b)의 임의의 근방에 f(a, b)>f(P), f(a, b)<f(Q) 만족하는 점 P, Q가 모두 존재하면(극대도 극소도 아니므로 극값이 아님)
f는 (a, b)에서 안장점 (a, b, f(a, b))를 갖는다고 한다.
대표적 예시로 이해를 도우면, 쌍곡 포물면의 안장점을 들 수 가있다.

미분적분학 공부할 때 써둔 건데 진짜로 맞는 건지는.. 사실 잘 모르겠다
*일변수 함수에서의 극대, 극소
[ 어떤 열린 구간 I에 속하는 모든 x에 대하여, f(a)>=f(x)가 성립하면, f(a)는 f의 극대 값
f(a)<=f(x)가 성립하면, f(a)는 f의 극소값이라고 한다. ]
경사가 0 벡터인 지점을 임계점(critical point)라고 하며,
이는 지역 최솟값이 아닐지라도 존재한다. (지역 최소에서만 경사가 0인 것은 아님)

그림을 보면 이해가 쉬울 것이다. (지역 최대와 지역 최소는 SGD에서 별 큰 문제가 되지 않는 것을 알았으므로 우리에게 문제는 지역 최소도 지역 최대도 아닌 평평한 구간=안장점)
잠재적으로 다루기 어렵지만 치명적이지는 않은 평평한 구간을 안장점(saddle point)라고 부른다. (지역 최소, 지역 최대 둘 다 아님)
함수의 차원이 높을수록 (모델에 파라미터가 많을수록) 지역 최솟값보다 안장점이 기하급수적으로 많을 가능성이 크다.
그 이유는 아래 그림과 같이 오차 함수가 1차 함수로 표현되었을 때,
임계점은 3가지 중 하나의 형태를 취할 수밖에 없다

그렇다면, 일차원 함수에서 임의의 임계점이 주어졌을 때, 이 점이 지역 최솟값일 확률은 1/3이라는 것이다.
예를 들어 전체 k개의 임계점이 있다면 총 k/3개의 지역 최솟값을 기대할 수 있다.
이를 더 높은 차원(d차원)으로 확장하면
임계점을 잡을 때, 해당 임계점이 지역 최소인지, 최대인지 안장점인지 알아내는 것이 조금 까다롭다.
어느 쪽에서 보느냐에 따라 달라지기 때문이다.

다음 그림을 보면 AB로 보면 지역 최소이고, CD로 보면 지역 최대이기 때문이다.
지역 최소이려면 d차원의 파라미터 공간상에서 d개의 다른 축상 임계점을 통과하도록 잘랐을 때(일차원 부분 공간으로 표현됨) 모든 부분에서 지역 최솟값으로 나타내어진다면, 해당 임계점은 지역 최솟값이 될 것이다.
일차원 부분 공간에서는 3가지 중 하나로 나뉠 수 있다는 사실에 착안하면,
d차원에서 임의의 함수의 임게점일 확률은 1/3^d인 것을 알 수 있다.
k개의 임계점을 가진다면, 임의의 함수는 k/3^d개의 지역 최솟값을 가진다고 예상할 수 있다.
즉, 이는 다시 말하면
함수의 차원이 높을수록 (모델에 파라미터가 많을수록) 지역 최솟값보다 안장점이 기하급수적으로 많을 가능성이 크다.
오차 곡면의 평평한 부분들은 다루기 어렵지만, 궁극적으로 SGD가 좋은 해로 수렴하는 것을 막지는 못한다.
하지만 경사가 0인 지점을 직접 해결하려는 시도는 심각한 문제를 일으키는데, 이로 인해 딥러닝 모델에 대한 특정 이차 최적화 방법들의 유용성이 떨어지고 있다. (이에 대해서는 나중에 자세히)
<지금 까지를 한번 정리해보면>
심층 신경망 학습에 큰 장애가 되는 것은 지역최솟값(+ 경사가 0이 되는 부분들) 과 어느 방향으로 결정할지 정하는 것에 대한 문제점 두개였다.
오랫동안 학자들은 지역최솟값이 가장 큰 장애라고 생각했으나, 오늘날에 도달하여 지역최솟값과 경사가 0이 되는 안장점과 같은 부분들은 SGD상에서 큰 장애가 되지 않는다는 실험적 결과들이 많이 나오게 되었다.
그렇다면, 진짜 장애는 어느방향으로 결정할지에 대한 문제이다.
이에 대해서 다루어 보도록 하겠다.
4.6 잘못된 방향의 경사
원래 여기서 부터 글을 다시 써야하는게 맞는데.. 알고보니까 4단원을 건너뛰고 5단원을 했어야 했네요 ㄱ-...
그러한 개인 사정으로 인해 4단원은 여기서 잠시 중단하고 5단원~7단원 내용부터 하고 시간이 나면 돌아오는걸로 하겠습니다.
www.youtube.com/watch?v=itEoe_m3Cpo
<참고자료>
- Greedy layer-wise training
[머신러닝] 15. 머신러닝 학습 방법(part 10) - AutoEncoder(2)
쉽게 읽는 머신 러닝 – 학습방법 (part 10) – AutoEncoder2 지난 10월 말 Facebook은 “Style Trans...
blog.naver.com
- Vanishing gradient problem
Vanishing Gradient Problem
어디서 많이 들어봤죠? | 이 글은 아래 Rohan Kapur의 글을 번역한 것입니다. 한국어로된 아티클 중에 일부 Vanishing Gradient Problem을 설명한 글이 있습니다만, 저는 좀 더 디테일하고 친절한 글로 Vanish
brunch.co.kr
tensorflow.blog/2016/04/18/fundamental-of-deep-learning-preview/
‘Fundamental of Deep Learning’ Preview
O’Reilly에서 텐서플로우와 관련된 첫 번째 책인 ‘Fundamental of Deep Learning’이 2016년 말에 출간 예정입니다. 지금은 Early Release 단계로 미리 구입해서 PDF나 이북 리더기로 읽으실 수 있습니다. 이 ��
tensorflow.blog
www.youtube.com/watch?v=QkjY-DgnAXc
'ML' 카테고리의 다른 글
| [딥러닝의 정석]05. 합성곱 신경망-2 (0) | 2020.08.03 |
|---|---|
| [딥러닝의 정석] 05. 합성곱 신경망-1 (0) | 2020.08.02 |
| [딥러닝의 정석]03. 텐서플로로 신경망 구현하기-2 (0) | 2020.07.21 |
| [딥러닝의 정석]03. 텐서플로로 신경망 구현하기 (0) | 2020.07.18 |
| [딥러닝의 정석]02. 전방향 신경망 학습 (0) | 2020.07.12 |



